Preparing for the Fundamentals of Engineering Exam (FEE) can be challenging, but having the right practice materials makes all the difference. This blog provides a free set of carefully curated sample MCQs with detailed answers and explanations to help you master key concepts and boost your confidence. Whether you’re reviewing core engineering subjects or practicing problem-solving techniques, these questions are designed to guide you toward exam success. Start your preparation today with these free resources!
FEE Free Sample MCQs with Answer and Explanation Part 1 (Civil)
1. A steel bar comprises three sections of three cross sections as shown in Fig. Q1. The diameters of parts AB, BC, and CD are 25 mm, 15 mm, and 35 mm respectively. The bar is subjected to an axial tensile force of 5 kN. If Young’s modulus of steel is 200 kN/mm2, and the elongations of the three sections of the bars are Δ1, Δ2, and Δ3 respectively, calculate the ratio of the largest to the smallest of these three elongations.
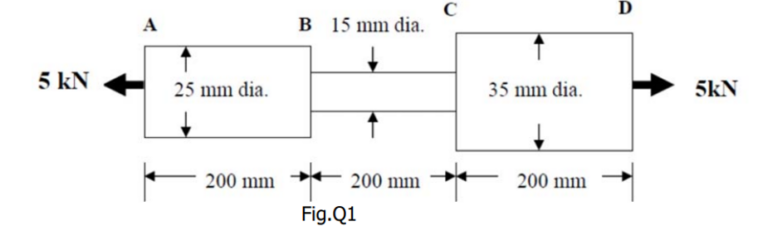
(a) 1.96
(b) 2.33
(c) 5.44
(d) 2.77
2. Three plane trusses are shown in Fig.Q2. The statical determinacy of the trusses, (1), (2) and (3) are respectively:

(a) determinate, indeterminate, unstable
(b) determinate, determinate, unstable
(c) determinate, indeterminate, determinate
(d) indeterminate, indeterminate, determinate
3. Three plane trusses are shown in Fig.Q2. The statical determinacy of the trusses, (1), (2) and (3) are respectively:
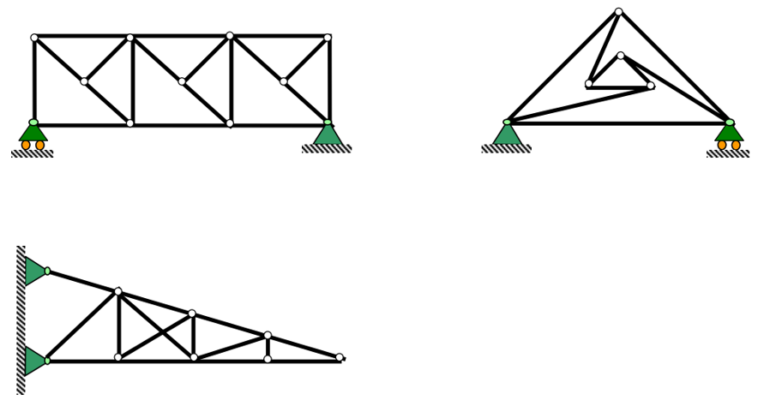
(a) determinate, indeterminate, unstable
(b) determinate, determinate, unstable
(c) indeterminate, indeterminate, determinate
(d) determinate, indeterminate, determinate
4. An axial load of 100 KN is acting on the stepped bar as shown below. If Young’s modulus of steel is 200 kN/mm2 What is total elongation?
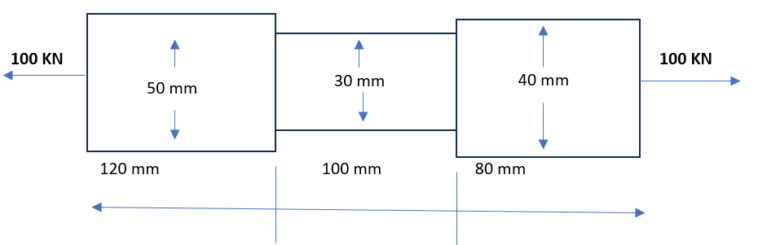
a. 0.833 mm
b. 4.154 mm
c. 0.133 mm
d. 1.236 mm
5. The static indeterminacy of the beams, (1), (2), (3), and (4) shown in Fig.Q3 are respectively:
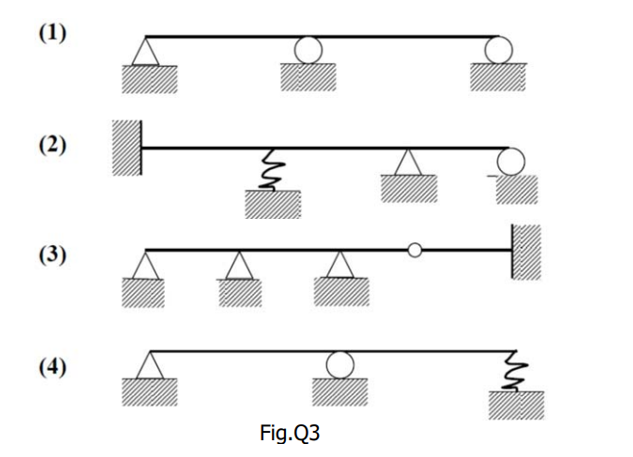
(a) 1, 4, 5, 1
(b) 2, 4, 5, 2
(c) 1, 4, 5, 2
(d) 1, 5, 4, 1
6. The static indeterminacy of the below beam
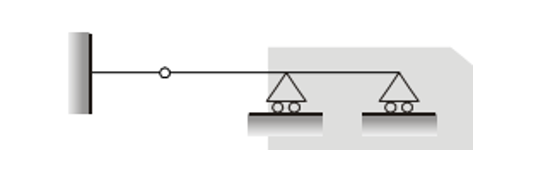
a. 2
b. 3
c. 4
d. 0
7. The degree of kinematic indeterminacy of the frame shown in the figure ignoring the axial deformation is given by
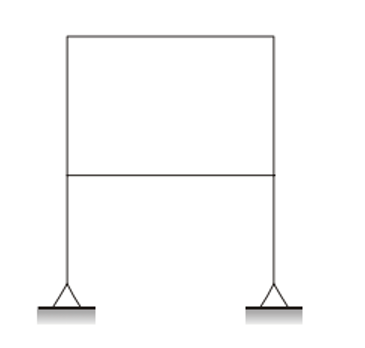
a. 8
b. 10
c. 12
d. 14
8. The degree of static indeterminacy of the given below is
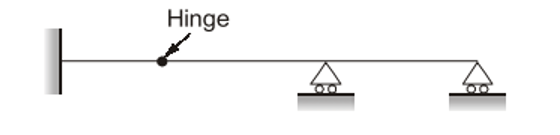
a. zero
b. one
c. two
d. three
9. A reinforced concrete column shown in Fig.Q4 supports a load of 10 kN. The load is shared between the steel reinforcement and the concrete. The crosssectional areas and Young’s moduli are: Ac = 1 x 104 mm2 and Ec = 20 kN/mm2 As = 200 mm2 and Es = 210 kN/mm2 What is the force carried by the steel reinforcement?
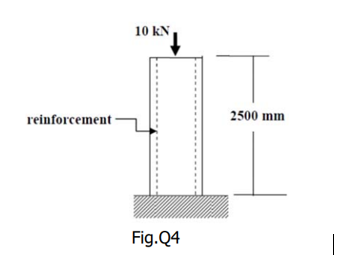
(a) 1.96 kN
(b) 2.74 kN
(c) 2.96 kN
(d) 1.74 kN
10. If seawater is used in place of potable water to cast OPC concrete, the effect is to
a. increase its strength;
b. reduce its strength;
c. retard setting;
d. decrease its durability.
Of the above,
(a) 1 and 3 are correct
(b) 2 and 3 are correct
(c) 2 and 4 are correct
(d) 1 and 4 are correct
11. A river is 3m deep and the river bed consists of a thick deposit of clay with a saturated unit weight of 20kN/m3. What is the effective stress of the clay layer at a depth of 3m below the river bed level?
(a) 30 kN/m2
(b) 60 kN/m2
(c) 90 kN/m2
(d) 120 kN/m2
12. During the site investigation for a deep foundation design, you discover in the borehole a layer of soft clay 5m deep where you had expected a hard stratum at the estimated depth of pile toe. Which of the following actions would you take? (a) Bore an extra 5m deeper than the original plan (b) Stop boring and move to the next borehole location (c) Continue boring until stronger soil is found (d) Abandon the site
13. In the figure below, what is the gauge pressure of air inside the closed container?

19,620 N/m2
(b) 13,873 N/m2
(c) 16,991 N/m2
(d) Cannot be determined
14. A 1:20 scale river model is designed based on Froude number similarity. What is the prototype flow velocity which corresponds to a model-measured velocity of 0.5 m/s?
Given Froude number
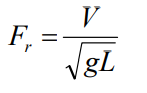
a. 10 m/s
b. 158.1 m/s
c. 2.24 m/s
d. None of the above
Answer with an explanation:
1. Ans c
To solve this problem, we calculate the elongation ( Δ Δ) of each section of the steel bar using the formula for axial deformation:
Δ = 𝐹 𝐿/ 𝐴 𝐸
Where:
- F=5kN=5000N is the tensile force.
- L = Length of the bar section (assumed to be the same for all sections in this problem).
- A=πd2/4= is the cross-sectional area of the section.
- E=200 kN/mm2=200×103 N/mm2 is Young’s modulus of steel.
Step 1: Relationship Between Elongation and Area
- Since F, L, and E are constant across all sections, the elongation is inversely proportional to the cross-sectional area:
- Δ ∝ 1/A
- And since A=πd2/4
- Δ ∝ 1/d2
Step 2: Calculate the Ratios of Elongations
For the three sections of the bar:
Section AB: dAB=25 mm
Section BC: dBC=15 mm
Section CD: dCD=35 mm
The elongations are inversely proportional to the square of the diameters:
Δ1:Δ2:Δ3=1/(25)2:1/(15)2:1/(35)2
Simplify the squares:
Δ1:Δ2:Δ3=1/625:1/225:1/1225
Step 3: Normalize and Identify the Largest and Smallest Elongations
The proportional elongations are:
ΔBC>ΔAB>ΔCD
The ratio of the largest elongation (ΔBC\ΔBC) to the smallest elongation is:
=1/225 ÷1/1225
=1225/225= 5.44
2. The answer is c
Solution:
For Fig 1.
m=5, r=3,j=4
m+r=5=3=8 =2j
Since m+r=2j, the truss is determinate
For Fig 2.
m = 9
r = 4
j = 6
m + r = 13
2j=12
Since m+r>2j The truss is statically indeterminate
For fig 3.
m = 9
j=6
r=3
m+r= 12
2j=12
Since m+r=2j The truss is determinate
3. The answer is d
For fig 1
Since b = 19, r = 3, j = 11, then b + r = 2j or 22 = 22. Therefore, the truss is statically determinate.
For fig 2
Since b = 15, r = 4, j = 9, then b + r > 2j or 19 > 18. The truss is statically indeterminate
For fig 3
Since b = 9, r = 3, j = 6, then b + r = 2j or 12 = 12. The truss is statically determinate.
4. Ans is c. 0.133 mm
Section 1:
P = 100 KN
d1 = 50 mm
l1= 120 mm
A1= d2π/4 = 502π/4 = 1963.5 mm2
σ 1 = P/A1 = 100 * 103 /1963.5 =50.93 N/mm2
now Δl1/l1 = σ 1/E
Δl1 = l1 σ 1/E
= 50.93 * 120/2 * 105
= 0.0305 mm
Similarly for section 2:
σ 2 = P/A2 = 100 * 103 / 302π/4
=141.47 N/mm2
Δl2 = l2 σ 2/E = 0.0707 mm
Similarly for section 3:
σ 3 = 79.58 N/mm2
Δl3 = l3 σ 3/E
=0.0318 mm
Total elongation = Δl = Δl1 + Δl2+ Δl3
= 0.0305 mm + 0.0707 mm + 0.0318 mm
= 0.133 mm
5. Correct option: (a) 1, 4, 5, 1.
To determine the static indeterminacy of the beams (1), (2), (3), and (4) in Fig. Q3, we will analyze each beam individually using the following formula:
Ds = R−E
Where:
- R = Total number of reactions provided by supports.
- E = Total number of equilibrium equations (in 2D, E=3).
Beam (1):
Supports:
- One hinged support (2 reactions: vertical and horizontal).
- Two roller supports (each providing 1 vertical reaction).
- Total R=2+1+1=4
Static indeterminacy: Ds=R−E=4−3=1
Beam (2):
Supports:
- One fixed support (3 reactions: vertical, horizontal, and moment).
- One spring support (1 vertical reaction).
- One hinged support (2 reactions: vertical and horizontal).
- One roller support (1 vertical reaction).
- Total R=3+1+2+1=7
Static indeterminacy: Ds=R−E=7−3=4
Beam (3):
Supports:
- Two hinged supports (each with 2 reactions: vertical and horizontal).
- One roller support (1 vertical reaction).
- One fixed support (3 reactions: vertical, horizontal, and moment).
- Total R=2+2+1+3=8
Static indeterminacy: Ds=R−E=8−3=5
Beam (4):
Supports:
- One hinged support (2 reactions: vertical and horizontal).
- One roller support (1 vertical reaction).
- One spring support (1 vertical reaction).
- Total R=2+1+1=4
Static indeterminacy: Ds=R−E= 4−3=1
Final Answer:
The static indeterminacy for the beams is:
- (1): Ds=1
- (2): Ds=4
- (3): Ds=5
- (4): Ds=1
6. Answer is a. 2
Solution:
Total reactions R:
R= 3(fixed support)+1(roller support 1)+1(roller support 2)=5
Static Indeterminacy Formula
The formula for static indeterminacy is:
Ds=R−E
For a 2D system, there are E=3
Substitute the values:
Ds=5−3=2
7. The answer is a. 8
Solution:
J=6, m=6, r=4
Dk = 3*6-4-6=8
8. The answer is b. one
Solution:
Ds= re+3m-rr-3(j+j1)
re= 3+1+1=5
m=3, j=3, j1=1
The hinge will create 2 members
Number of internal reaction components released.
rr=1
Ds= 5+9-1-3*(3+1)
=1
9. Ans is d. 1.74 kN
Solution:
Step 1: Write the Relation Between Strain and Stress
The strain is given by: ε=σ/E
where:
- σ: Stress
- E: Young’s modulus
For concrete (ccc) and steel (sss):
εc=εs
σc/Ec=σs/Es
Ac/EcFc=As/ EsFs


≈8.26kN
Now, calculate Fs:
Fs=P−Fc=10−8.26=1.74 kN
10. The correct options are:
- Reduce its strength, 4. Decrease its durability
Explanation:
When seawater is used in place of potable water to cast OPC (Ordinary Portland Cement) concrete, the following effects occur:
Reduction in strength (Option 2):
Seawater contains salts, especially chlorides, and sulfates, which can interfere with the hydration process of cement. These salts lead to a reduction in long-term strength compared to concrete made with potable water.
Decrease in durability (Option 4):
Chlorides in seawater can initiate and accelerate corrosion of reinforcement steel within the concrete, significantly reducing its durability. Sulfates in seawater can also react with the cement paste, causing expansion and cracking over time.
11. Answer a. 30 kN/m2
Solution:
Effective Stress (σ’) = σ−u
Where u= γw⋅hw
γw=9.81kN/m3 (unit weight of water)
hw=3 m
σ=γ⋅h
where:
- γ=20kN/m3 (saturated unit weight of clay)
- h=3m
on putting values
20kN/m3 *3m – 9.81kN/m3 *3m = 60-29.43
=30.57 kN/m2
12. The correct answer is: (c) Continue boring until stronger soil is found
Explanation:
When designing deep foundations, the pile toe needs to rest on a strong stratum (e.g., dense sand, gravel, or rock) to provide adequate bearing capacity and limit settlement. Discovering soft clay at the expected depth indicates the presence of unsuitable soil for supporting the foundation.
Actions explained:
(a) Bore an extra 5m deeper than the original plan: This assumes a hard stratum lies exactly 5m deeper, which is not confirmed and may lead to an incomplete investigation.
(b) Stop boring and move to the next borehole location: This could result in missing critical data and might not ensure a proper foundation design.
(c) Continue boring until stronger soil is found: This is the most logical action, as the objective is to locate a suitable load-bearing stratum for the deep foundation.
(d) Abandon the site: This is not practical unless the entire site investigation suggests that no suitable foundation can be constructed.
13. Answer is b. 13,873
Solution:
Steps to Solve:
Gauge Pressure Definition:
Gauge pressure is the pressure measured relative to atmospheric pressure.
Observations from the Diagram:
- The height of the water column in the inclined pipe determines the pressure difference.
- The water column rises to a vertical height of h, which can be calculated using the inclined length (2 m ) and the angle of 45∘
h=2m⋅sin(45∘)= 2*0.707=1.414 m
Hydrostatic Pressure:
- The pressure exerted by the water column is: P=ρ⋅g⋅h,
where:
- ρ=1000 kg/m3 (density of water),
- g=9.81 m/s2(gravitational acceleration),
- h=1.414 m
= 1000*9.81*1.414
= 13,871.34 Pa
≈ 13.87 kPa
14. The answer is c. 2.24 m/s
Solution:
Relationship Between Prototype and Model:
The velocity and length scale relationship between the model and prototype can be derived as:
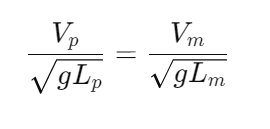
where:
- Vp = prototype velocity,
- Vm=0.5 m/s(model velocity),
- Lp=20Lm(since the scale ratio is 1:20).
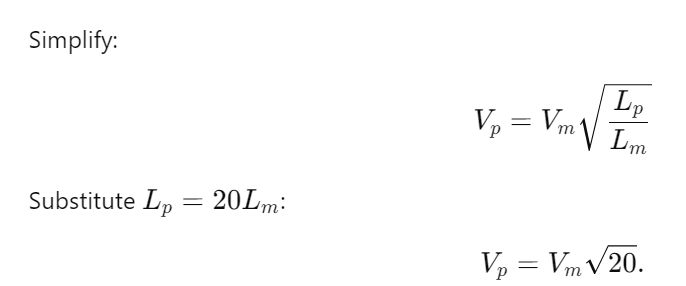
Substitute Known Values:
0.5 * 4.472=2.236m/s






